Birthdates demo using Gaussian Processes, demo_births, R

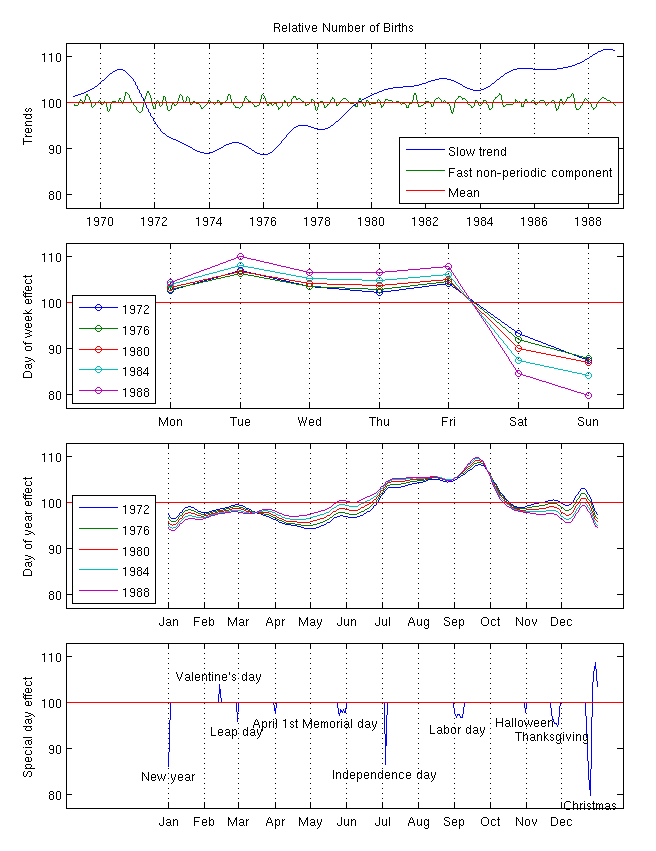
Demonstration of analysis of birthday frequencies in USA 1969-1988 using Gaussian process with several components. Demonstration includes two parts a) analysis of data having sum of births for each day of year and b) analysis for whole time series. Data source: National Vital Statistics System natality data, as provided by Google BigQuery and exported to cvs by Chris Mulligan (sum data http://chmullig.com/wp-content/uploads/2012/06/births.csv) and Robert Kern (whole time series http://www.mechanicalkern.com/static/birthdates-1968-1988.csv)

Code

Analysis of data having sum of births for each day of year

require(RcppOctave)

# load data
d <- read.csv('birthdates-1968-1988.csv')

# target and covariate
y <- d$births
n <- length(y)

# fixed special days in USA
specdays <- cbind(
		c(1,1,2,2,4,7,7,10,12,12,12,12,12,12,12,12,12,12),
		c(1,2,14,29,1,4,5,31,22,23,24,25,26,27,28,29,30,31))

# construct additional covariates for fixed special days
xs <- matrix(0,n,nrow(specdays))
xsw <- matrix(0,n,nrow(specdays))
for (i1 in 1:nrow(specdays)){
	xs[,i1] <- as.numeric(d$month==specdays[i1,1] & d$day==specdays[i1,2])
	xsw[,i1] <- as.numeric(d$month==specdays[i1,1] & d$day==specdays[i1,2] & d$day_of_week>=6)
}

# construct additional covariates for floating special days
uyear <- unique(d$year)
xss <- matrix(0,n,3)

# Labor day
for (i1 in 1:length(uyear)){
	q <- which(d$year==uyear[i1] & d$month==9&d$day_of_week==1)
	xss[q[1],1] <- 1
	xss[q[1]+1,1] <- 1
}

# Thanksgiving
for (i1 in 1:length(uyear)){
  q <- which(d$year==uyear[i1] & d$month==11 & d$day_of_week==4)
  xss[q[4],2] <- 1
  xss[q[4]+1,2] <- 1
}

# Memorial day
for (i1 in 1:length(uyear)){
  q <- which(d$year==uyear[i1] & d$month==5 & d$day_of_week==1)
  xss[tail(q,1),3] <- 1
}

# Combine covariates
x <- cbind(1:n,xs,xsw,xss)
m <- ncol(x)

# Normalize
xn <- x

# Pass variables to Octave:
.O$m <- m
.O$n <- n
.O$x <- x
.O$xn <- xn
.O$yn <- scale(y)
.O$ymean <- mean(y)
.O$ystd <- sd(y)
.O$d <- d

# Construct the model in Octave:
o_source(text="
	% priors
	pl = prior_logunif();
	pn = prior_logunif();

	% smooth non-periodic component
	gpcf1 = gpcf_sexp('lengthScale', 365, 'magnSigma2', .7, 'selectedVariables', 1);
	% faster changing non-periodic component
	gpcf2 = gpcf_sexp('lengthScale', 10, 'magnSigma2', .4, 'selectedVariables', 1);
	% periodic component with 7 day period
	gpcfp1 = gpcf_periodic('lengthScale', 2, 'magnSigma2', .1, ...
                      'period', 7,'lengthScale_sexp', 20, 'decay', 1, ...
                      'lengthScale_prior', pl, 'magnSigma2_prior', pl, ...
                      'lengthScale_sexp_prior', pl, 'selectedVariables', 1);
	% periodic component with 365.25 day period
	gpcfp2 = gpcf_periodic('lengthScale', 100, 'magnSigma2', .1, ...
                      'period', 365.25,'lengthScale_sexp', 1000, 'decay', 1, ...
                      'lengthScale_prior', pl, 'magnSigma2_prior', pl, ...
                      'lengthScale_sexp_prior', pl, 'selectedVariables', 1);
	% linear component for special days
	gpcfl=gpcf_linear('coeffSigma2',1,'selectedVariables',2:m);

	% Gaussian model
	lik = lik_gaussian('sigma2', 0.1, 'sigma2_prior', pn);

	% construct the model
	gp = gp_set('lik', lik, 'cf', {gpcf1, gpcf2, gpcfp1, gpcfp2, gpcfl});
")

# optimise the hyperparameters (MAP), this might take several hours(!)
o_source(text="
	opt=optimset('TolFun',1e-3,'TolX',1e-4,'Display','iter');
	gp=gp_optim(gp,xn,yn,'opt',opt);
")

# Predictions and training log predictive density + loo-cv
o_source(text="
	[Eft, Varft, lpyt] = gp_pred(gp, xn, yn);sum(lpyt)
	[Efl, Varfl, lpyl] = gp_loopred(gp, xn, yn);sum(lpyl)
")


# Predictions for different components
o_source(text="
	[Eft1, Varft1] = gp_pred(gp, xn, yn, 'predcf', 1);
	[Eft2, Varft2] = gp_pred(gp, xn, yn, 'predcf', 2);
	[Eft3, Varft3] = gp_pred(gp, xn, yn, 'predcf', 3);
	[Eft4, Varft4] = gp_pred(gp, xn, yn, 'predcf', 4);
	[Eft5, Varft5] = gp_pred(gp, xn, yn, 'predcf', 5);
")

# Pass results back to R:
Eft1 <- .O$Eft1
Eft2 <- .O$Eft2
Eft3 <- .O$Eft3
Eft4 <- .O$Eft4
Eft5 <- .O$Eft5

# plot results (in Octave)
o_source(text="
	figure
	set(gcf,'units','centimeters');
	set(gcf,'pos',[35 2 18.5 24]);
	set(gcf,'papertype','a4','paperorientation','portrait',...
	'paperunits','centimeters','paperposition',[ 0 0 21.0 29.7]);
	clf

	subplot(4,1,1)
	% reshape 7 day periodic component
	ywft3s=reshape(Eft3(1:7301),7,1043)';
	ywft3s=ywft3s(:,[6:7 1:5]);
	% trend is not completely seprated to the first smooth component so
	% compute the trend in the 7 day periodic component
	trend3=interp1(3:7:7303,mean(ywft3s'),1:n)';

	% Eft1+trend3 = smooth trend from component 1 plus trend from the
	%               7 day periodic component
	% Eft2 = faster changing non-periodic component
	plot(x(:,1),denormdata(Eft1+trend3,ymean,ystd)/ymean*100,x(:,1),denormdata(Eft2,ymean,ystd)/ymean*100)
	set(gca,'xtick',1+cumsum([0+365 365+365 366+365 365+365 366+365 365+365 366+365 365+365 366+365 365+365]),'xticklabel',1970:2:1988,'xgrid','on','xlim',[-100 7405])
	ylim([77 113])
	line(xlim,[100 100],'color', 'r')
	legend('Slow trend','Fast non-periodic component','Mean',4)
	ylabel('Trends')
	title('Relative Number of Births')

	subplot(4,1,2)
	% compute index for start of each year
	ywys=reshape(d.year(1:7301),7,1043)';
	ywys=ywys(:,[6:7 1:5]);
	Y=1969:1988;
	for i1=1:numel(Y);
	  qi(i1)=find(ywys(:,1)==Y(i1),1);
	end

	% detrend the first periodic component (note that this trend was
	% added to smooth trend above)
	ywft3s=denormdata(ywft3s,ymean,ystd)/ymean*100;
	mywft3s=mean(ywft3s,2);
	ywft3s=bsxfun(@minus,ywft3s,mywft3s)+100;

	% ywft3s = 7 day periodic component at different years
	plot(ywft3s(qi(4:4:end),:)','-o')
	set(gca,'xtick',1:7,'xticklabel',{'Mon' 'Tue' 'Wed' 'Thu' 'Fri' 'Sat' 'Sun'},'xgrid','on')
	xlim([-.5 7.5])
	ylim([77 113])
	line(xlim,[100 100],'color', 'r')
	legend('1972','1976','1980','1984','1988',3)
	ylabel('Day of week effect')
	
	subplot(4,1,3)
	% reshape 365.25 day periodic component
	Y=1969:1988;
	yyft4s=NaN+zeros(20,366);
	for i1=1:numel(Y);
	  for i2=1:366
	    q=Eft4(d.year==Y(i1)&d.day_of_year==i2);
	    if ~isempty(q)
	      yyft4s(i1,i2)=q;
	    end
	  end
	end
	yyft4s=denormdata(yyft4s,ymean,ystd)/ymean*100;

	% yyft4s = 365.25 day periodic component at different years
	plot(yyft4s(4:4:end,:)','-')
	set(gca,'xtick',1+cumsum([0 31 29 31 30 31 30 31 31 30 31 30]),'xticklabel',{'Jan' 'Feb' 'Mar' 'Apr' 'May' 'Jun' 'Jul' 'Aug' 'Sep' 'Oct' 'Nov' 'Dec'},'xgrid','on','xlim', [-86 388])
	line(xlim,[100 100],'color', 'r')
	ylim([77 113])
	legend('1972','1976','1980','1984','1988',3)
	ylabel('Day of year effect')

	% reshape special day component
	for i1=1:366
	  yft5(i1,1)=mean(Eft5(d.day_of_year==i1));
	end

	subplot(4,1,4)
	% yft5 = special day effect
	plot(denormdata(yft5,ymean,ystd)/ymean*100,'-')
	set(gca,'xtick',1+cumsum([0 31 29 31 30 31 30 31 31 30 31 30]),'xticklabel',{'Jan' 'Feb' 'Mar' 'Apr' 'May' 'Jun' 'Jul' 'Aug' 'Sep' 'Oct' 'Nov' 'Dec'},'xgrid','on','xlim', [-86 388])
	line(xlim,[100 100],'color', 'r')
	ylabel('Special day effect')
	ylim([77 113])
	yft5d=denormdata(yft5,ymean,ystd)/ymean*100;
	h=text(1,yft5d(1),'New year','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(45,yft5d(45),'Valentine''s day','HorizontalAlignment','center','VerticalAlignment','bottom');
	h=text(60,yft5d(60),'Leap day','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(92,yft5d(92),'April 1st','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(148,yft5d(148)-1,'Memorial day','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(186,yft5d(186),'Independence day','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(248,yft5d(248)-1,'Labor day','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(305,yft5d(305),'Halloween','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(328,yft5d(328)-1.5,'Thanksgiving','HorizontalAlignment','center','VerticalAlignment','top');
	h=text(360,yft5d(360),'Christmas','HorizontalAlignment','center','VerticalAlignment','top');
	drawnow;
")